卡方分布 | 轨迹

概念

若n个相互独立的随机变量ξ₁，ξ₂，…,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布）$N(0,1)$，则这n个服从标准正态分布的随机变量的平方和$Q=\sum_{i=1}^n \xi_i^2$构成一新的随机变量$\chi^2$，其分布规律称为卡方分布（chi-square distribution）。n为自由度，自由度不同就是不同的卡方分布。

若$X_1,X_2,…,X_n$是$N(\mu,\sigma^2)$的随机变量，则$\sum_{i=1}^n(X_i-\bar X)^2\sim \sigma^2\chi_{n-1}^2$,其中$\bar X=\frac {1}{n}\sum_{i=1}^n X_i$

若$X_i \sim N(\mu_i,\sigma^2_i),i=1,…,k$,则卡方分布为：$\sum_{i=1}^k(\frac{X_i-\mu_i}{\sigma_i})^2$

卡方分布用途

检查实际结果与期望结果之间何时存在显著差异。

检验拟合优度，也就是说检验一组给定数据与指定分布的吻合程度。如：用来检验两幅图像的点对是否符合H（计算得到的单应矩阵），是否是内点。

自由度，即用于计算检验统计量$\chi^2$的独立变量的数目。如点，由$(x,y)$表示，自由度为2.
显著性，卡方分布指出观察与期望之间差异显著性（个人认为可以理解为观察与期望明显不符出现的概率，如外点出现的概率5%），使用显著性水平进行检验，常用的显著性水平为1%和5%。
如何检验？
卡方分布使用的是单尾检验且是右尾，右尾被作为拒绝域。通过查看检验统计量$\chi^2$是否位于右尾的拒绝域内，来判断期望分布得出的结果。如下图：
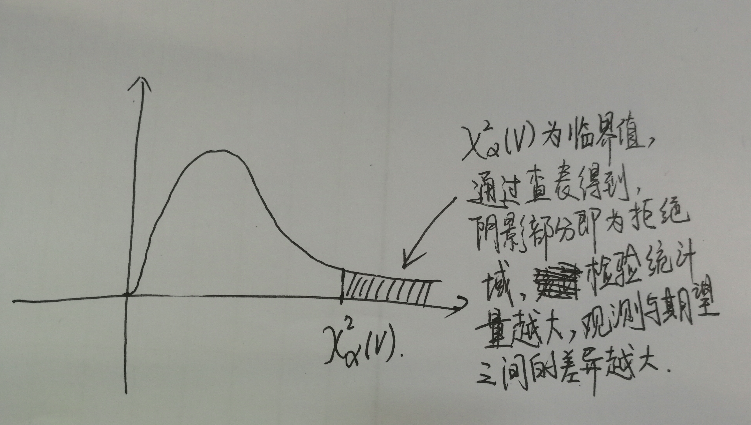
卡方临界值表是给定可以查询的。

最后一行即显著性水平。